이전 글에서 간단하게 GNN의 기본 개념에 대해서 알아보았다.
이전 글 : (Graph Neural Net)GNN basic
Graph Neural Net (GNN) Basic
최근 그래프 구조 데이터를 분석하는 능력으로 딥러닝에서 촉망 받고 있는 그래프 신경망, 과연 무엇을 학습시키는 것이고 어떤 방식으로 학습이 이루어질까? 그리고, 이전에 나온 합성곱 신경
didi-universe.tistory.com
이제 GNN 알고리즘에 대해서 좀 더 딥하게 알아보자.
먼저 GNN의 시초라고 할 수 있는 Recurrent GNN에 대해 소개한다.
Recurrent Graph Neural Network

Original Graph Neural Network
GNN(graph neural network)은 Scarselli et al.의 The Graph Neural Network Model에서 처음 등장했다. https://ieeexplore.ieee.org/document/4700287
이 논문은 GNN을 이용하여 Node classification 하는 방식에 대해 다루었으며,
Node Classification에서 각 노드 v는 feature x_v로 특징지어지고 ground truth label인 t_v와 짝지어져있다. 일부만 라벨이 주어진 그래프 G에서 목표는 라벨이 주어진 노드들을 이용해서 나머지 라벨이 없는 노드들의 라벨을 알아맞추는 것이다.(semi-supervised learning과 비슷한 맥락)
- 기본 가정 : node는 objects or concepts을, edge는 their relationship을 represent함
각각의 concept은 그것의 속성이나 관계된 concept에 의해 정의됨

GNN의 동작은 따라서 크게 두가지로 생각할 수 있다.
1. propagation step - 이웃 노드들의 정보와 연결된 엣지 정보들을 토대로 현재 자신 노드의 상태를 표현, 업데이트 함
2. output step - task 수행을 위해 학습을 통해 얻은 노드 벡터(=node feature)를 입력으로 하여 output을 출력함. ex) node label classification 이라면 node label이 아웃풋
이를 수식으로 표현하면 아래와 같다.
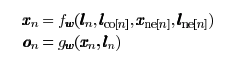
propagation step과 output step
ln : 점 n의 feature
lco[n] : 점 n과 연결된 선들의 feature
lne[n] : 점 n과 연결된 점들의 feature
xne[n] : 점 n과 연결된 점들의 상태
fw는 input값들을 d-dimensional 공간으로 매핑하는 propagation fuction (본 논문에서는 transition fuction이라 표현함), gw는 output function을 말한다.
이처럼 fw으로 점의 상태 xn을 업데이트 하고 k번 반복 후에 마지막 상태(xn)와 특징(ln)을 사용하여 결과값(on)을 출력한다.
Learning algorithm : Banach fixed point theorem
그렇다면 어떻게 학습이 이뤄질까?
위에서 설명한 Motivation : GNN ≈CNN에서 Multi-layer를 GNN에 사용하면 얻는 이점은 layer가 깊어질수록 직접적으로 연결된 이웃 노드 이외에 멀리 있는 노드들의 영향력을 고려하여 현재 노드의 feature를 구성할 수 있다고 했다.
이렇게 멀리있는 노드에서부터 현재 노드까지 정보가 전달되는 과정을 message passing이라고 한다. message passing이란 개념은 GNN이 등장하고 난 이후에, Gilmer et al.의 “Neural message passing for quantumchemistry” 에서 등장했다. 해당 논문은 여러 종류의 GNN 구조를 일반화하는 프레임워크를 message passing 이라는 것으로 제안한 논문이다.
하지만, 초기 GNN은 multi-layer 구조가 아니기 때문에 불가능하다. 따라서, Banach fixed point theorem에 따라, iterative method로 고정된 node feature를 찾는다.
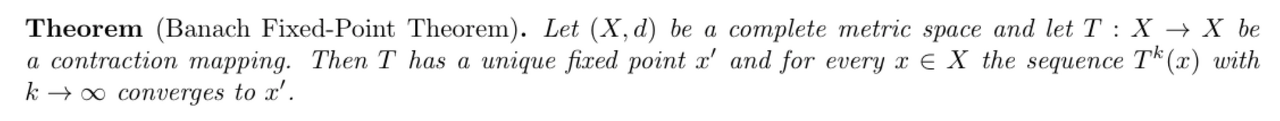
Banach Fixed-Point Theorem
k가 크면, x에 매핑 T를 k번 적용한 값과 k+1번 적용한 값이 거의 같다는 의미로
간단히 말하자면 어떠한 조건하의 매핑은 유일한 point를 갖고 모든 점에 대해 이 매핑을 무한번 적용하면 그 유일한 point로 수렴한다는 것이다.
(T가 contraction mapping인 것을 이용해 귀납법을 사용해 증명)
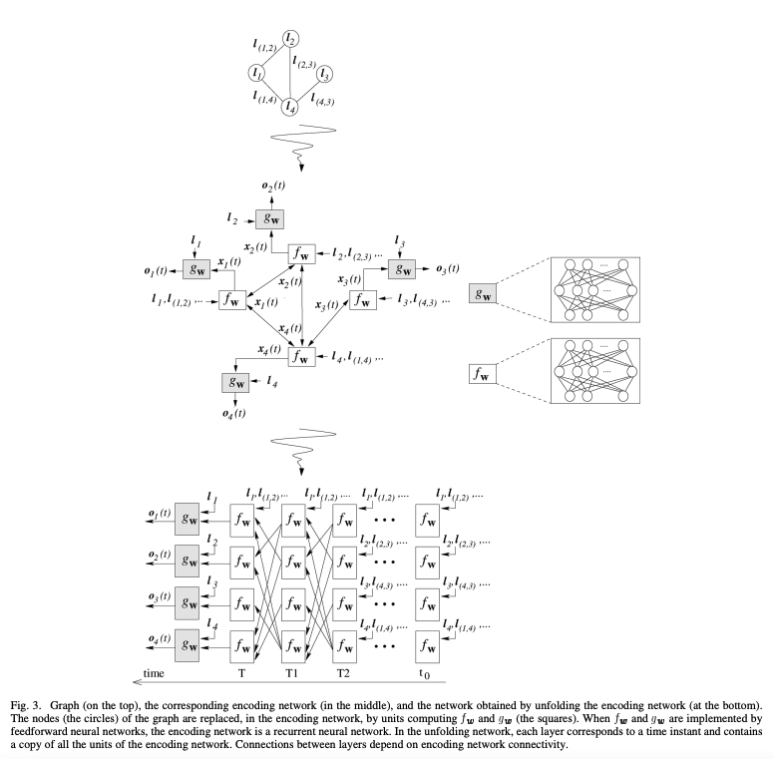
fw와 gw가 업데이트 되는 과정
xn과 on이 어떤 수렴된 값을 가지려면, Banach fixed point theorem에 의해 propagation function이 contraction map이어야 한다고 정의되어 있다.
이 Banach finxed point theorem을 이용하여 iterative method식으로 위 수식을 전개하면 아래와 같이 전개할 수 있다.
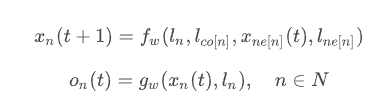
학습 방법은 이웃 노드들의 information을 recurrent하게 전달하여 node state를 업데이트 한다. 이 과정을 node state가 수렴할 때까지 iteration을 반복해야 한다.
fixed 된 xn,on을 얻으면 loss를 계산할 수 있고, gradient 계산을 통해 weight을 업데이트한다. 여기서 weight은 Fw의 파라미터이다. neural network 라면 network의 가중치가 된다.
그럼 다음으로 GNN 알고리즘 중에 하나인 Spational convolutional Network 에 대해 알아보겠다.
다음 글 : GNN 알고리즘 (2) - Spational convolutional Network
GNN 알고리즘 - (2) Spatial Convolutional Network
Spatial Convolutional Network 이미지 분류와 이미지 영역 구분에 많이 쓰이는 Convolutional Neural Network(CNN)의 아이디어와 비슷하며 기존 convolution 방식과 거의 동일하고 graph convolution으로 표기하기도 한
didi-universe.tistory.com
참고자료
https://ralasun.github.io/deep%20learning/2021/02/11/gcn/
Introduction to Graph Neural Network - GNN 소개 및 개념 · Ralasun Resarch Blog
Introduction to Graph Neural Network - GNN 소개 및 개념 11 Feb 2021 | graph-neural-network 이번 포스팅을 시작으로, Graph Neural Network(GNN)에 대해 본격적으로 다루도록 하겠습니다. 이번 포스팅은 Graph Neural Network가
ralasun.github.io
'AI > GNN' 카테고리의 다른 글
| GNN 알고리즘-(3)Spectral Convolutional Network (Spectral methods) (0) | 2022.04.14 |
|---|---|
| GNN 알고리즘 - (2) Spatial Convolutional Network (2) | 2022.04.13 |
| Graph Neural Net (GNN) Basic (0) | 2022.04.13 |


댓글